View Foci Of Rectangular Hyperbola Images. For two given points, the foci, a hyperbola is the locus of points such that the difference between the distance to each focus is constant. In mathematics, a hyperbola (listen) (adjective form hyperbolic, listen) (plural hyperbolas, or hyperbolae (listen)) is a type of smooth curve lying in a plane.
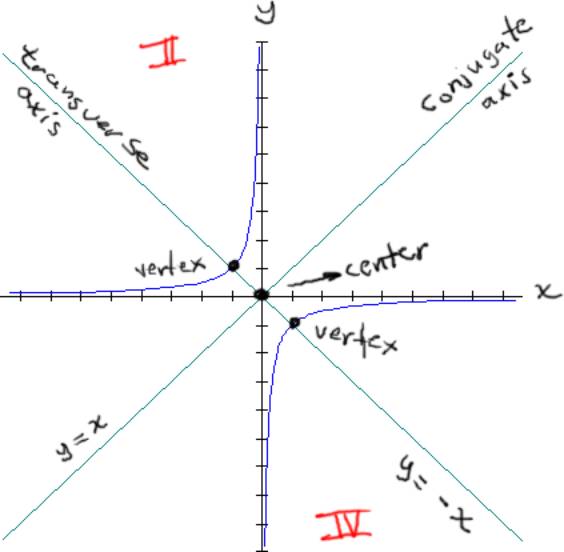
At large distances from the foci, the hyperbola begins to approximate two lines the rectangular hyperbola with the coordinate axes as its asymptotes is given by the equation xy=c if one forms a rectangle with vertices on the asymptotes and two sides that are tangent to the hyperbola, the length.
The formula to determine the focus of a parabola is just the pythagorean theorem. Graph of a hyperbola function, showing asymptotes and vertices of the hyperbola. A hyperbola is two curves that are like infinite bows. A rectangular hyperbola is a hyperbola with eccentricity sqrt2 ≈ 1.4142.


